Simulator and Inverse Dynamics
Framework and Simulator
To be able to manage the project code properly, it’s best to have all the stuff fit in a framework. By searching through the internet, I find two matlab repositories related to Contact Invariant Optimization. I tried both, only the first one works for me.
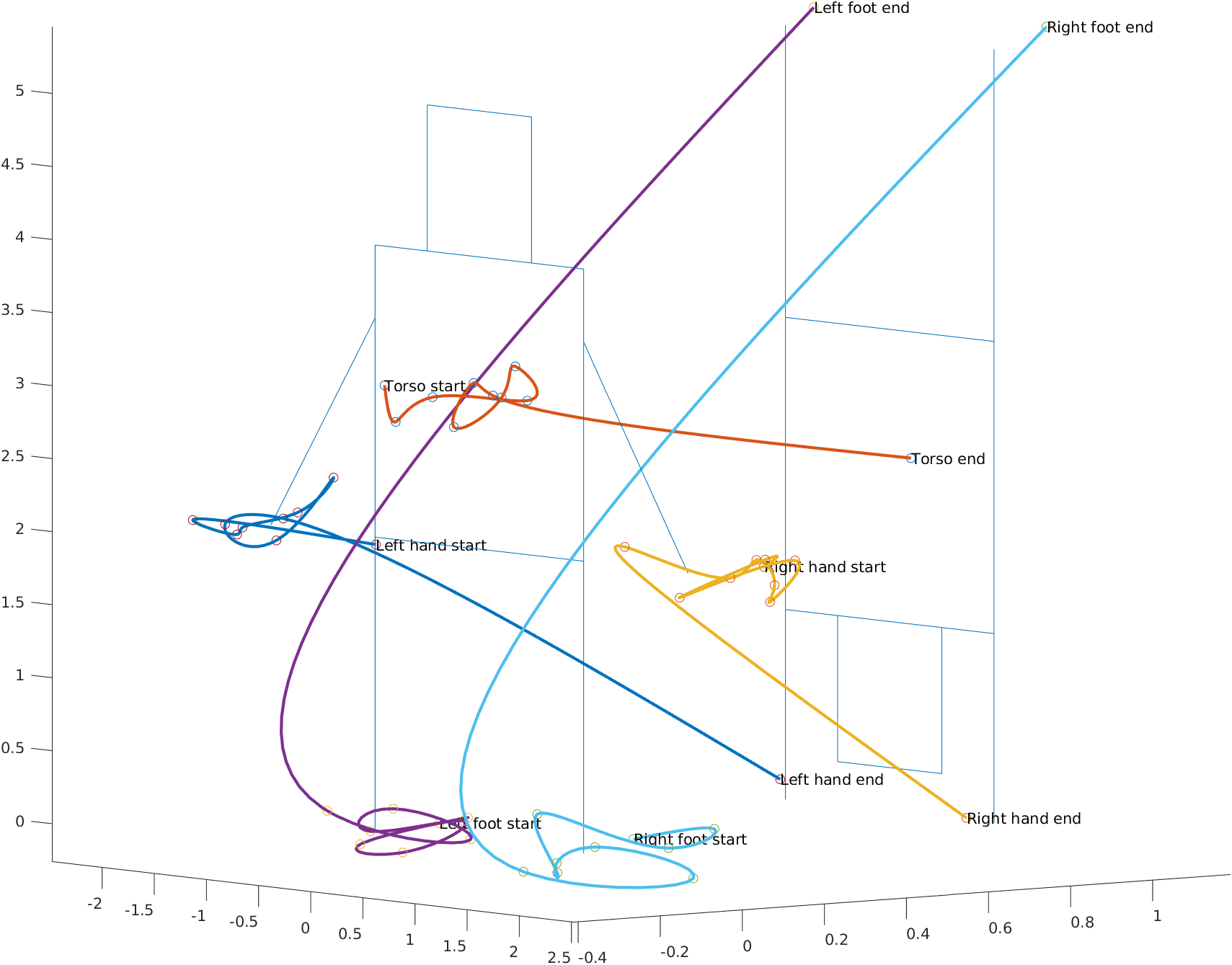
This codebase is very clean and direct, which make it easy to get started with. By running the code, I get the following trajectory.
However, I decide not to base my code onto this project, because I notice that the whole codebase takes an ad-hoc architecture. For example, the dynamics model used is fully hand-crafted and fixed, and what even worse is that, this model is hard coded into the cost function! This means that in future if I’d switch to a new model, I will have to rewrite the whole thing!
But this doesn’t mean that it’s useless. Instead, since it’s specifically written for re-implementing the paper, I can find every formula with its corresponding code and also some implementation details not mentioned in the paper. That helps me understand the algorithm better.
The ideal framework needs to have a physics simulator and a bunch of available models, and it would better to provide functions to calculate some essential properties of the model (such as inertia matrix). Also it’s better to align with some degree of “standard” (like supporting common robot description file format, being compatible with off-the-shelf optimization packages, etc.)
Finally I choose pyrobolearn as the framework.
Its advantages include:
- Supporting the
Bulletsimulator - Dozens of robot models
- Interfaces which are unified and easy to use
- Plenty of implemented control algorithms
- Having a place left for CIO (although not implemented yet)
- Being well documented
Here is a screenshot I took from the simulator.

Since the framework hasn’t implemented CIO yet, I have to do it by myself.
Inverse Dynamics
The most complex formulas in the paper are to recover the contact forces and actuated controls using inverse dynamics. First define the following symbols:
- Given $q$ the character pose (torso pose concatenated with joint positions)
- Let $N$ be the number of end-effectors (usually 4)
- Let $D$ be the degree of freedom ($D = \dim (\dot{q})$)
- Let $J(q) \in \mathbb{R}^{6N \times D}$ be the Jacobian matrix mapping $\dot{q}$ to contact-space velocities.
- Let $B$ be the matrix modulating the control signals
The formula relates the inverse dynamics $\tau(q, \dot{q}, \ddot{q})$, contact forces $f$ and control signals $u$ is given by
\[\tau(q, \dot{q}, \ddot{q}) = J(q)^{\mathrm{T}} f + B u\]The process of recovering $f$ and $u$ is done by minimizing the squared residual of the equation above subject to (linearized) friction cone and the squared regularization of $f$ and $u$.
To be able to do this, I need to calculate the inverse dynamics $\tau$ first.
Luckily, pyrobolearn provides a function Robot.calculate_inverse_dynamics to do this.
However, things don’t go right when I try it on robots with floating base.
The program crashes and leaves me with an error message, just as this issue mentioned.
By doing what it suggests doesn’t make sense, either, since the result it returns contains 7 more elements more than the degree of freedom, but I am expecting 6.
Even worse, the flags argument I pass doesn’t have any documentation describing it.
It turns out that’s not even a problem of the pyrobolearn framework, but Bullet’s.
I have to look into Bullet’s source code to see how the function is handled there.
- I go to the implementation of inverse dynamics, and it suggests that the floating base only adds 6 more dimensions. This makes sense to me, but is inconsistent with the result I am given.
- I find the code relates to python API, but still don’t find the
flagsargument. - Finally I find the python command processing code. It turns out that when the
flagsis set to 1, it uses so called “RBD model” instead. To have the normal mode (whenflagsis set to 0) work correctly, the dimensions of the input vectors ($q$, $\dot{q}$ and $\ddot{q}$) should include the additional degrees of freedom of the torso. Moreover, the code for preprocessing floating-based models seems to forget to populate itsqvector. I raise an issue and fix it on my own.
I then test the results by applying the calculated $\tau(q, \dot{q}, 0)$ directly onto the torques of joints to see whether that compensates the gravity, and it goes good.
Next Step
After solving the issue in the framework, I can continue implementing CIO. There are several things I need to do next week:
- Figure out how to formulate $J(q)$
- Formulate the physics cost and the contact invariant cost
- Figure out how to use
cvxoptto do quadratic programming